Объем цилиндра: формула и расчет
Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем.
Расчет объема цилиндра
Слово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:
- Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее под прямым углом.
- Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
- Цилиндр — геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одной из его сторон.
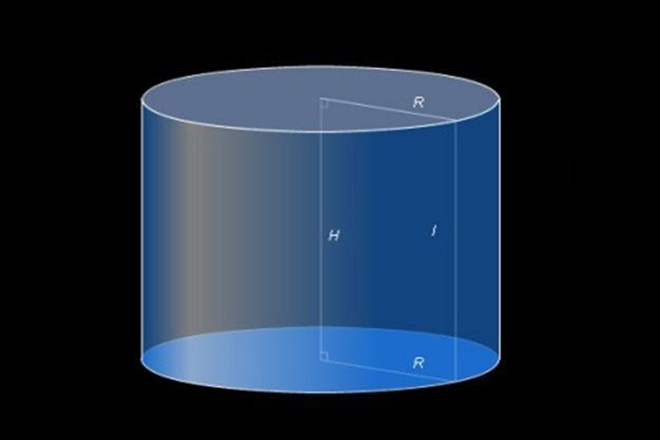
Все эти определения верны. Также стоит отметить основные части цилиндра:
- Основания — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
- Боковая поверхность цилиндра — поверхность между плоскостями оснований.
Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т.д.
Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой.

Есть и другие общие понятия для цилиндров:
- Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны.
- Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
- Радиусом цилиндра называется радиус его основания.
- Высотой цилиндра называется расстояние между плоскостями оснований.
- Осью цилиндра называется прямая, проходящая через центры оснований.
- Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
- Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.
Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту.
V = πR2h,
где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14.
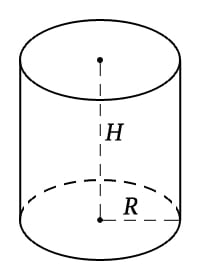
Таким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d.
V = πhd2/4
Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S.
V = n * S
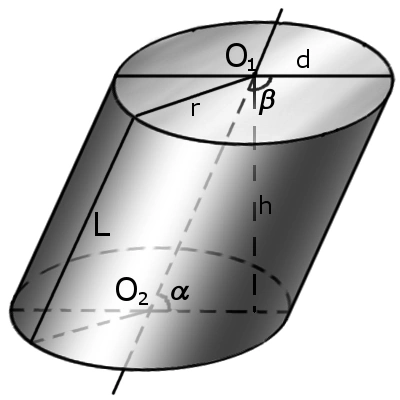
Если цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле:
V = S * n * sin α
Исчисляется объем цилиндра в кубических единицах.
Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими:

Радиус цилиндра равен радиусу сферы — R. Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
V = 2R * πR2
Приведя формулу к должному виду получим:
V = 2πR3
Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем.

В этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле:
V = πh(a/2)2
Где применяется расчет объема цилиндра
Расчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Объем таких цилиндрических предметов исчисляется в литрах.

Рассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства.
Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму.

Архитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль.


