Самое большое число

Продолжительное время пользовался популярностью слух о том, что престижнейшую в мире премию не присуждают математикам исключительно потому, что Альфред Нобель некогда из-за представителя «братства цифр и формул» пережил неприятный казус — якобы супруга «взрывного» предпринимателя с помощью упомянутого милого человека снабдила мужа развесистыми рогами.

Люди, привыкшие в меньшей мере доверять фантазии и слухам, предполагают: причина в том, что в математике, как науке прикладной, никаких свершений уже не будет — все открыто, и прорыва ждать не приходится. Но в пику мертвому Нобелю «адепты логарифмов» продолжают пытаться доказать, что математика — это не только инструмент для вычислений, а нечто большее, и продолжают находить и изучать новые аспекты любимой науки, стремясь, например, отыскать самое большое число — о чем и пойдет речь ниже.

Невозможное возможно, если сильно захотеть

Возможно, некоторые люди неоднократно задавались вопросом о том, есть ли самое большое число, после которого счет останавливается. И если нечто подобное в математике присутствует, то любопытно узнать, как выглядит, записанное в цифрах, а еще лучше — звучит «по-русски» (или на другом языке). Найти ответ на первую поставленную пытливым умом задачу труда не составит — стоит только вспомнить школьный курс, чтобы понять: если к сколь угодно впечатляющему числу прибавить единицу, то в итоге получено будет число на единицу большее — и так бессчетное количество раз. Напрашивается вывод: поиск самого большого числа в мире — занятие бесконечное, как минимум.

Однако математики нечто подобное искать продолжают и — что любопытно! — находят. Дело в том, что в собственных поисках эти деятели руководствуются не некой абстрактной и недостижимой целью — отыскать самое большое возможное число. Работы ведутся в десятках направлений и с оговорками: ищут то предельного размера число с собственным названием и значением, то максимальное среди простых (натуральных (целых положительных), делящихся только на самих себя и 1), то рекордное из применяемых в математических вычислениях. Другими словами, делают возможное, чтобы не скучать и доказывать целесообразность существования всевозможных математических институтов и профильных факультетов.

О колониальных войнах и русской душе

Заводя разговор о самом большом числе, не обойтись без возвращения к основам, чтобы упростить понимание, ведь большинство людей после окончания института или училища вряд ли пользовались вычислениями сложнее уровня «3 ящика на 7 человек».

В мире используют два способа наименования чисел — английский и американский. Первый получил большее распространение — в первую очередь потому, что бывшие колонии наследовали привычные принципы. Названия чисел тут образуются путем добавления к латинскому числительному (tres, quattuor, quinque и т. д.) суффикса «-иллион», а к следующему, большему в 1000 раз, — суффикса «-иллиард». Получается чередование: триллион-триллиард, квинтиллион-квинтиллиард. Выбивается из этого правила только первое число: «миллион» происходит от латинского «тысяча» с добавлением соответствующего суффикса — буквально «тысяча тысяч».

В американском способе именования, который распространен в Канаде, Франции и США, суффикс «-иллиард» не используется вовсе, а латинские числительные просто идут по возрастанию. Так получается, что английский «триллиард» равен американскому «квадриллиону», а вместо миллиардеров в США — биллионеры.

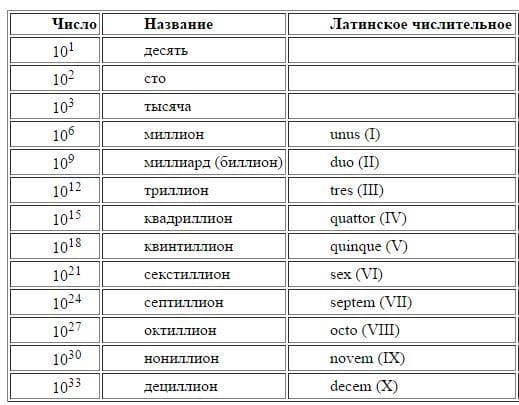
В России заимствовать не стеснялись — хотя считается, что в ходу тут американская система, по факту используют смесь: вместо «биллиона» стабильно вставляют в речь «миллиард», да и «триллиарды» периодически «всплывают».

По именам собственным

Разобравшись, как называется то или иное число в «международной системе координат», и поняв, почему переводчики всегда читают надписи в американских фильмах «неправильно», стоит перейти к следующей категории больших чисел — внесистемным.

Оперируя латинскими числительными, можно и дальше продолжать именовать крупные числа, получая сложные составные названия, типа «септемдециллиона» или «октодециллиона». А вот имен собственных получится образовать только три штуки — «вигинтиллион» (10^63 — десять в 63 степени), «центиллион» (10^303) и «миллеиллион» (10^3003). Дальше у древних ромеев в цифрах «затык» — кончаются числительные. Так и выходит, что самое большое число, обладающее несоставным названием, — это 10^3003.

Но дальше к слово(или цифро-)образованию присоединились мыслящие умы, которые придумали давать собственные имена крупным числам, обладающим математическим значением или использующимся в расчетах, типа гравитационной постоянной или «пи». Так появились:

• мириада, которая описывает, в отличие от литературных «мириад», вполне конечное значение — 10000;
• гугол (10^100) и гуголплекс (10^гугол), придуманные в 1938 году Эдвардом Каснером с племянником;
• асанкхейя (10^140), над которым потрудились буддистские «собиратели праны» — монахи хранили уверенность, что столько космических циклов требуется для обретения истинного наслаждения, нирваны;
• первое число Скьюза (Sk1=e^(e^(e^79))), названное так в честь того, кто и придумал использовать его для доказательства гипотезы Риманна, и второе, которое еще больше (Sk2=10^(10^(10^1000))).

И масса других чисел, используемых в математике для всевозможных расчетов и доказательств, а также система сверхстепеней и другие способы записи столь громоздких значений, именуемые «нотациями».

Так просто, но так сложно

Еще одно направление изучения — поиск самого большого простого числа. Над этим проектом, получившим название Great Internet Mersenne Prime Search (GIMPS), работает Университет центрального Миссури — руководит программой Кертис Купер.

По состоянию на начало 2020-го самым большим простым считается найденное в рамках проекта 7 декабря 2018 года американским программным разработчиком Патриком Ларошем число, которое записывается как 2^82589933-1. Оно — 51-е в ряду чисел Мерсенна, вид которых — 2^n-1, где n — натуральное число. Находка Лароша состоит из 24 862 048 цифр, что на 1,6 миллиона больше, чем у 50-го числа Мерсенна, найденного в 2017 году, которое состоит из 23 249 425.

Проверку новое самое большое простое число прошло за 12 суток. За проделанную работу Патрик Ларош получил 3 тысячи долларов. Впереди у математиков новая цель — отыскать число Мерсенна из 100 миллионов цифр.

Устремленное в бесконечность

Однако перечисленные и неназванные числа покажутся неприметными и невпечатляющими по сравнению с числом Грэма (названо в честь создателя — американского математика Рональда Грэма), записанным в Книгу рекордов Гиннесса в качестве самого большого числа, которое использовалось в математике для доказательства важной гипотезы. Конкретно в этом случае речь идет о теории Фрэнка Рамсея, которая в кратком виде такова: если в N-мерном кубе, где вершины произвольно соединены красными и синими отрезками, закрашивать указанными цветами ребра, то до какого значения N возможно избежать окрашивания плоскости куба одним цветом.

Число Грэма, часто записываемое как G64 или G, приняли в 1977 году. При этом до сих пор математики не способны с достоверной точностью сказать, сколько в этом числе цифр и каких — известны только последние 50: …03222348723967018485186439059104575627262464195387. А вот первые едва ли удастся в обозримом будущем уточнить. Чего стоит только запись этого числа, состоящая из 64 уровней.

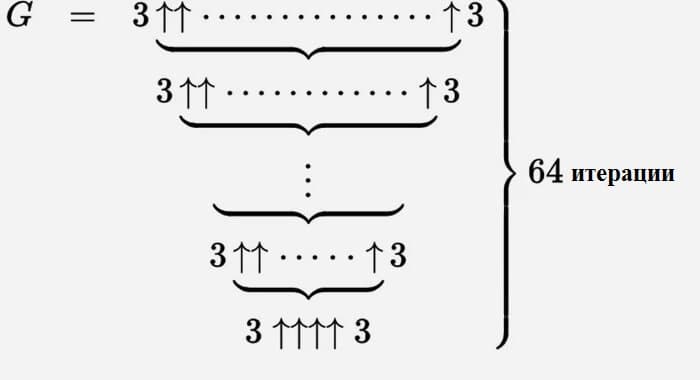
Потому не стоит удивляться, что это число иногда сравнивают с бесконечностью — для человеческого мозга разницы при отсчете этих двух величин никакой не будет.